Integration routines for Splines. More...

Classes
class	BilinearForm
	A bilinear form with user-provided operators. More...

class	LinearForm
	A linear form with a user-provided operator. More...

Typedefs
using	ScalarProduct = BilinearForm< operators::IdentityOperator, operators::IdentityOperator >

Functions
template<typename O2 >
	BilinearForm (O2 o2) -> BilinearForm< operators::IdentityOperator, O2 >
	Deduction guide for matrix element.

	BilinearForm () -> BilinearForm< operators::IdentityOperator, operators::IdentityOperator >
	Deduction guide for scalar product.

	LinearForm () -> LinearForm< operators::IdentityOperator >
	Deduction guide for an integral over a Spline.

template<size_t ordergl, typename T , typename F , size_t order1, size_t order2>
T	integrate (const F &f, const bspline::Spline< T, order1 > &m1, const bspline::Spline< T, order2 > &m2)
	Calculates matrix element of user-provided function.

Detailed Description

Integration routines for Splines.

Nampespace containing the integration routines. Analytical integration is represented by the linear and bilinear forms. There is also code for numerical integration using the boost fixed poind Gauss-Legendre scheme.

Typedef Documentation

◆ ScalarProduct

using bspline::integration::ScalarProduct = typedef BilinearForm<operators::IdentityOperator, operators::IdentityOperator>

Short hand for a scalar product

$\left\langle a,\, b\right\rangle = \left\langle a\,\middle|\,b\right\rangle = \int\limits_{-\infty}^{\infty} \mathrm{d}x~a(x) \,\,b(x).\$

Function Documentation

◆ BilinearForm() [1/2]

bspline::integration::BilinearForm ( ) -> BilinearForm< operators::IdentityOperator, operators::IdentityOperator >

Deduction guide for scalar product.

Deduction guide for a bilinear form which corresponds to the scalar product.

$\left\langle a,\, b\right\rangle = \left\langle a\,\middle|\,b\right\rangle = \int\limits_{-\infty}^{\infty} \mathrm{d}x~a(x) \,\,b(x)\$

◆ BilinearForm() [2/2]

template<typename O2 >

bspline::integration::BilinearForm ( O2 o2 ) -> BilinearForm< operators::IdentityOperator, O2 >

Deduction guide for matrix element.

Deduction guide for a bilinear form which corresponds to the matrix element of the operator 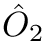$\hat{O}_2$ .

$\left\langle a,\, b\right\rangle = \left\langle a\,\middle|\,\hat{O}_2\,\middle|\,b\right\rangle = \int\limits_{-\infty}^{\infty} \mathrm{d}x~a(x) \,\,\hat{O}_2\,\,b(x)\$

.

Template Parameters

O2	Type of the operator applied to the second spline.

◆ integrate()

template<size_t ordergl, typename T , typename F , size_t order1, size_t order2>

T bspline::integration::integrate	(	const F &	f,
		const bspline::Spline< T, order1 > &	m1,
		const bspline::Spline< T, order2 > &	m2
	)

Calculates matrix element of user-provided function.

Calculates the 1D integral

$I=\int\limits_{-\infty}^{\infty} \mathrm{d}x~ m_1(x)\, f(x)\, m_2(x).$

The integral is evaluated numerically on each interval using boost's Gauss-Legendre scheme of order ordergl.

Parameters

f	Callable 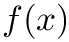to be multiplied to the integrand.
m1	First spline .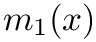
m2	Second spline .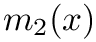

Template Parameters

ordergl	Order of the Gauss-Legendre integration scheme provided by the boost library.
T	Datatype of the calculation.
F	Type of the callable .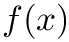
order1	Order of the spline .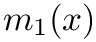
order2	Order of the spline .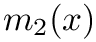

Exceptions

BSplineException If the two splines are defined on different grids.

Returns: The value of the integral .

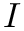
◆ LinearForm()

bspline::integration::LinearForm ( ) -> LinearForm< operators::IdentityOperator >

Deduction guide for an integral over a Spline.

Deduction guide for a linear form which represents the integral over the spline

$\left\langle a\right\rangle=\int\limits_{-\infty}^{\infty}\mathrm{d}x~a(x).$

Classes

Typedefs

Functions